| TTL и CMOS логика Цифровая схемотехника на логических микросхемах. Счетчики, сдвиговые регистры, простая логика... |
 11.08.2017, 05:03
11.08.2017, 05:03
|
|
|
Частый гость
Регистрация: 20.09.2014
Сообщений: 24
Сказал спасибо: 0
Сказали Спасибо 0 раз(а) в 0 сообщении(ях)

|
 Сумматор бинарных кодов Линг (Ling Adder)
Сумматор бинарных кодов Линг (Ling Adder)
Доброго времени суток!
В сети есть много сведений о сумматоре бинарных кодов Линг (Ling Adder). Однако логическую схему сумматора по этим сведениям не удаётся построить. Подскажите пожалуйста ресурс с готовой на 8-бит (16-бит) схемой Ling Adder.
|

|
|
|
 11.08.2017, 17:49
11.08.2017, 17:49
|
|
|
Модератор
Регистрация: 04.08.2010
Адрес: Москва СЗАО
Сообщений: 11,260
Сказал спасибо: 11,170
Сказали Спасибо 3,860 раз(а) в 2,930 сообщении(ях)

|
 Re: Сумматор бинарных кодов Линг (Ling Adder)
Re: Сумматор бинарных кодов Линг (Ling Adder)
Так у Huey Ling много работ в этой области.
Там ещё и улучшения от Samuel Naffziger из HP.
А про реализацию лучше смотреть отсюда.
__________________
rtfm forever должно быть основой для каждого. Альтернатива грустна, поскольку метод слепого щенка успешно работает при весьма малом числе вариантов…
Последний раз редактировалось mike-y-k; 11.08.2017 в 18:04.
|

|
|
|
 13.08.2017, 22:07
13.08.2017, 22:07
|
|
|
Частый гость
Регистрация: 20.09.2014
Сообщений: 24
Сказал спасибо: 0
Сказали Спасибо 0 раз(а) в 0 сообщении(ях)

|
 Re: Сумматор бинарных кодов Линг (Ling Adder)
Re: Сумматор бинарных кодов Линг (Ling Adder)
Спасибо.
В представленном ресурсе есть улучшения CLA по Лингу с тремя MUL в каждом разряде. Три MUL очевидно уже не актуально, обходятся одним MULем. Пример улучшения префиксного сумматора (PPA) на логическом уровне по Лингу с одним MUL есть, например, тут. Если улучшение есть, то должно бить, например, уменшение глубины схемы, или сокращение общего количества логических елементов, или оптимизация Fan-In (Fan-Out). Для таких выводов необходима готовая схема Ling Adder (любая из его работ) для сравнения, лучше представленная на дискретных логических елементах (можно будет воссоздать, проверить таблицей истинности), без NMOS (PMOS). Однако любая готовая схема Ling Adder, напримкр на 8-бит (16-бит) в сети не встечается. Может кому известно такое место?
Последний раз редактировалось Mishel 825; 13.08.2017 в 22:11.
|

|
|
|
 13.08.2017, 22:45
13.08.2017, 22:45
|
|
|
Почётный гражданин KAZUS.RU
Регистрация: 20.06.2006
Адрес: Украина, Запорожье
Сообщений: 8,016
Сказал спасибо: 0
Сказали Спасибо 4,954 раз(а) в 2,378 сообщении(ях)

|
 Re: Сумматор бинарных кодов Линг (Ling Adder)
Re: Сумматор бинарных кодов Линг (Ling Adder)
по тэгу ling adder гугло вываливает ling adder verilog code с картинками...
|

|
|
|
 14.08.2017, 02:04
14.08.2017, 02:04
|
|
|
Модератор
Регистрация: 04.08.2010
Адрес: Москва СЗАО
Сообщений: 11,260
Сказал спасибо: 11,170
Сказали Спасибо 3,860 раз(а) в 2,930 сообщении(ях)

|
 Re: Сумматор бинарных кодов Линг (Ling Adder)
Re: Сумматор бинарных кодов Линг (Ling Adder)
Mishel 825, очень долго прорабатывать цепочки ссылок на работы Ling, Naffziger и Co. Я за пару минут Вам подбросил статью с описанием алгоритма.
Если Вы таки подразумеваете уже разведённую реализацию или готовую схему - тогда нужно налаживать контакты с инженерами HP на их форуме и спрашивать там. Только есть шанс споткнуться о требования соглашения о неразглашении.
В своё время при работе ещё с HPIB было такое, до сих пор где-то папка с официальными бумагами лежит  .
Или очень последовательно по всем работам и ссылкам в них - возможно где-то в зоне .edu и есть нужное Вам.
Да и уважаемый jump вполне правильно указал на реализацию в вариациях FPGA/xPLD, сейчас такое на дисконтной логике уже не делают. Но описание в verilog вполне можно и в обычную схему перевести  .
__________________
rtfm forever должно быть основой для каждого. Альтернатива грустна, поскольку метод слепого щенка успешно работает при весьма малом числе вариантов…
Последний раз редактировалось mike-y-k; 14.08.2017 в 02:10.
|

|
|
|
 14.08.2017, 05:31
14.08.2017, 05:31
|
|
|
Частый гость
Регистрация: 20.09.2014
Сообщений: 24
Сказал спасибо: 0
Сказали Спасибо 0 раз(а) в 0 сообщении(ях)

|
 Re: Сумматор бинарных кодов Линг (Ling Adder)
Re: Сумматор бинарных кодов Линг (Ling Adder)
По тєгу ling adder verilog code нашел возможно наилучшее описание схемы, правда префиксного сумматора с использованием логики Линга. Здесь на рисунках не указано откуда заводить Hi для А в кружке, структура S в кружке не раскрыта.
mike-y-k, Ling Adder интересует в связи с величиной глубины его схемы. Известно, например, что 8-bit Kogge-Stone PPA имеет глубину 9 елементов. Если Линг улучшил структуру префиксного сумматора, то его схема очевидно должна иметь глубину, напримет, 8 елементов.
Последний раз редактировалось Mishel 825; 14.08.2017 в 05:33.
|

|
|
|
 14.08.2017, 12:44
14.08.2017, 12:44
|
|
|
Модератор
Регистрация: 04.08.2010
Адрес: Москва СЗАО
Сообщений: 11,260
Сказал спасибо: 11,170
Сказали Спасибо 3,860 раз(а) в 2,930 сообщении(ях)

|
 Re: Сумматор бинарных кодов Линг (Ling Adder)
Re: Сумматор бинарных кодов Линг (Ling Adder)
Mishel 825, собственно там везде схема описана логическими функциями. Дальше просто ее в verilog и зашить в FPGA на отладочной плате. Ну или ручками Нарисовать на россыпи из этих уравнений состояния.
Дальше уже рутинный процесс тестирования.
__________________
rtfm forever должно быть основой для каждого. Альтернатива грустна, поскольку метод слепого щенка успешно работает при весьма малом числе вариантов…
|

|
|
|
 15.08.2017, 20:43
15.08.2017, 20:43
|
|
|
Почётный гражданин KAZUS.RU
Регистрация: 25.11.2010
Адрес: г. Дзержинск Нижегородская обл.
Сообщений: 1,734
Сказал спасибо: 130
Сказали Спасибо 1,115 раз(а) в 530 сообщении(ях)

|
 Re: Сумматор бинарных кодов Линг (Ling Adder)
Re: Сумматор бинарных кодов Линг (Ling Adder)
Сообщение от mike-y-k

|
|
Дальше просто ее в verilog и зашить в FPGA на отладочной плате
|
Да-же в железо не обязательно. Обкатать такую схему на симуляторе - сильно упростит процесс.
|

|
|
|
 16.08.2017, 02:22
16.08.2017, 02:22
|
|
|
Модератор
Регистрация: 04.08.2010
Адрес: Москва СЗАО
Сообщений: 11,260
Сказал спасибо: 11,170
Сказали Спасибо 3,860 раз(а) в 2,930 сообщении(ях)

|
 Re: Сумматор бинарных кодов Линг (Ling Adder)
Re: Сумматор бинарных кодов Линг (Ling Adder)
DanilinSA, ну это уже ТС виднее. Академическую задачу можно и в симулятре посмотреть (при отсутствии жёстких требований), а вот с реальным сигналом уже так просто не получится - только прикидка алгоритма.
__________________
rtfm forever должно быть основой для каждого. Альтернатива грустна, поскольку метод слепого щенка успешно работает при весьма малом числе вариантов…
|

|
|
|
 23.08.2017, 02:25
23.08.2017, 02:25
|
|
|
Частый гость
Регистрация: 20.09.2014
Сообщений: 24
Сказал спасибо: 0
Сказали Спасибо 0 раз(а) в 0 сообщении(ях)

|
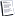 Re: Сумматор бинарных кодов Линг (Ling Adder)
Re: Сумматор бинарных кодов Линг (Ling Adder)
Используя описания тут и тут с небольшой доработкой получилась схема Ling Adder на 8 бит (приложил). Для этой схемы алгебраическое выражение управляющего сигнала Нi зависит от парности разряда. Это даёт сокращение нескольких логических улементов. В таком виде глубина схемы 8-bit Ling Adder равна 9 елементов. Для сравнения - глубина схемы 8-bit Kogge-Stone PPA равна 10 елементов.
Улучшения от Samuel Naffziger из HP представлены частично схемой SMOS. Для выводов необходимо переводить SMOS в дискретную схему, тогда появится «комфортная» уверенность в чём заключаются улучшения схемы Ling Adder.
|

|
|
|
 Ваши права в разделе
Ваши права в разделе
|
Вы не можете создавать новые темы
Вы не можете отвечать в темах
Вы не можете прикреплять вложения
Вы не можете редактировать свои сообщения
HTML код Выкл.
|
|
|
Часовой пояс GMT +4, время: 07:10.
|
|